65537 (number)

← 65536
65538 →
65537
Cardinal sixty-five thousand five hundred thirty-seven
Ordinal 65537th
(sixty-five thousand five hundred thirty-seventh)
Factorization prime
Divisors 2
Roman numeral LXVDXXXVII
Binary 100000000000000012
Octal 2000018
Duodecimal 31B1512
Hexadecimal 1000116

65537 is the integer after 65536 and before 65538.

In mathematics

65537 is the largest known prime number of the form 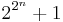2^{2^{n}} %2B1, where 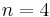n = 4. In number theory, primes of this form are known as Fermat primes, named after the mathematician Pierre de Fermat. To date, the only prime Fermat numbers are

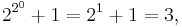
2^{2^{0}} %2B 1 = 2^{1} %2B 1 = 3,

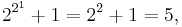
2^{2^{1}} %2B 1= 2^{2} %2B1 = 5,

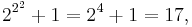
2^{2^{2}} %2B 1 = 2^{4} %2B1 = 17,

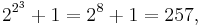
2^{2^{3}} %2B 1= 2^{8} %2B 1= 257,

and the largest known Fermat prime,

2^{2^{4}} %2B 1 = 2^{16} %2B 1 = 65537.[1]

In 1732, Euler found that the next Fermat number is composite:

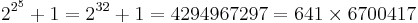
2^{2^{5}} %2B 1 = 2^{32} %2B 1 = 4294967297 = 641 \times 6700417

In 1880, F. Landry showed that

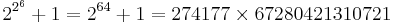
2^{2^{6}} %2B 1 = 2^{64} %2B 1 = 274177 \times 67280421310721

Applications

65537 is commonly used as a public exponent in the RSA cryptosystem. This value is seen as a wise compromise, since it is famously known to be prime, large enough to avoid the attacks to which small exponents make RSA vulnerable, and can be computed extremely quickly on binary computers, which often support shift and increment instructions. Exponents in any base can be represented as shifts to the left in a base positional notation system, and so in binary the result is doubling - 65537 is the result of incrementing shifting 1 left by 16 places, and 16 is itself obtainable without loading a value into the register (which can be expensive when register contents approaches 64 bit), but zero and one can be derived more 'cheaply'.

References

  1. ^ Conway, J.H., and R.K. Guy. (1996). The Book of Numbers. New York: Springer-Verlag Inc. p. 139.